If I gave you a discount to immediately pay off your loans this week, would you take it?
Is it better to take the discount today, or pay the amount over time instead?
One of my readers recently asked me a question about PTPTN (Malaysian Government education) loan repayment. His question was about using credit cards to pay for the PTPTN loan — which unfortunately isn’t possible right now.
But when I was talking to him, he made me think about evaluating a discounted loan offer.
So this one is for you and me. How do you know when to take a discount or not?
Hypothetical Situation 1:
Aaron owes $20,000 to the Government. They’ll give him a 20% discount if he pays up Immediately. If not, he has 10 years to pay at 0% interest.
This is the simplest of the three situations we’ll discuss today.
Let’s first pretend that Aaron has $16,000 easily available and that the Government gives out 0% interest loans (yeah right).
Should Aaron immediately grab the discount? On paper, the 20% discount looks attractive. It looks like it’s the only right decision.
But it’s an interesting question, because if Aaron doesn’t take the discount — he still has $16,000 available. What could he use it for? Perhaps as downpayment for a brand new BMW? Or a new Rolex? Or if he’s financially savvy, he could invest the money instead — generating profits. Would Aaron be able to generate enough profits over 10 years to make up for losing his 20% discount?
For the purposes of our calculation, let’s assume Aaron can earn 5% profits every year on his investments.
Let’s now compare the two scenarios:
Scenario A: Take the 20% Discount. Pay $16,000 Today
20% discount on $20,000 = $4,000. So we have to pay $16,000 today.
Let’s call that Present Value Payment of $16,000.
Savings = $4,000
Scenario B: Invest $16,000. Pay $20,000 Over 10 Years
Yearly payment = $2,000
Initial cash = $16,000
Interest rate = 5%
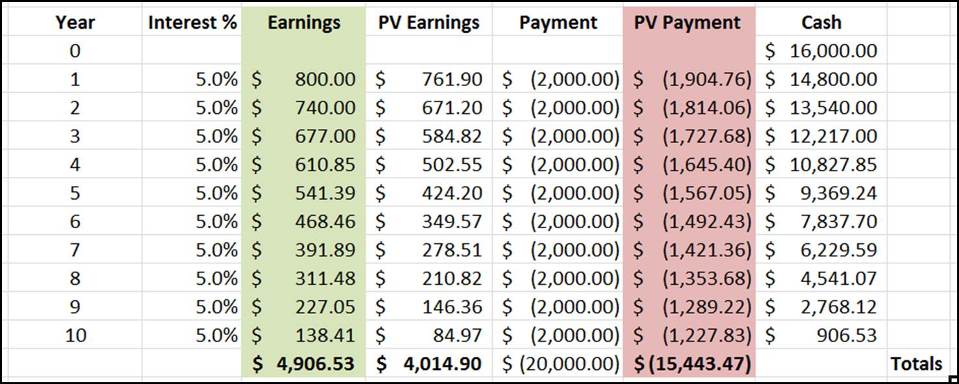
The table above calculates Aaron’s cashflow over 10 years. Assuming he doesn’t add any more money in, we can immediately see a few things:
- Aaron has had to pay $4,000 more than in scenario A. Total payment here is $20,000.
- But total earnings from investments is $4,906.53.
- So at the end, Aaron still has $906.53 left over in the bank
Scenario B is obviously better than Scenario A. The initial investment of $16,000 has made enough profit to cover the full loan amount of $20,000, with a nice leftover in the bank.
The crucial element here is the interest rate of 5%. Can Aaron consistently get that? What if he only gets a very safe Fixed Deposit rate every year of 3.6%?
Scenario C: Invest $16,000. Pay $20,000 Over 10 Years. Expected Returns Lower
Yearly payment = $2,000
Initial cash = $16,000
Interest rate = 3.6%
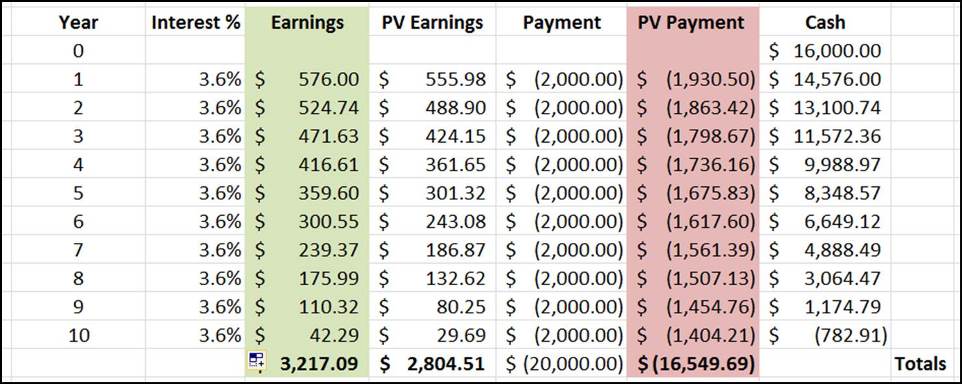
Here, we can see that Aaron loses. It would have been better to take the initial 20% discount:
- Aaron runs out of money in year 10. His investments have not made enough profit to cover the loan payments.
- Total earnings is only $3,217.09. Compare that to the $4,000 we would have saved in Scenario A.
The drop from 5% to 3.6% interest looks small, but over a period of time — it makes a significant difference.
Key Learning: How much you expect to make on investments (interest rate) affects your financial decisions
Hypothetical Situation 2:
Aaron owes $40,000 to the Government. They’ll give him a 20% discount if he pays up this week. If not, he has 15 years to pay at 1% interest.
Here things get a little more challenging.
Not only is the loan amount bigger, now the Government is doing what Governments do: charging interest.
What kind of interest? Let’s assume it’s fixed flat rate per annum interest. Which is similar to a typical car loan in Malaysia. (It’s my understanding that all PTPTN loanholders since June 2008 also have this kind of interest). Note that home loans are usually reducing balance loans — which is different from what we’re talking about here.
How will this new factor affect our evaluation? Let’s see:
Scenario A: Take the 20% Discount. Pay $32,000 Today
20% discount on $40,000 = $8,000. So we have to pay $32,000 today.
Present Value Payment = $32,000
Savings = $8,000 (immediate) + $6,000 (on interest) = $14,000
Scenario B: Invest $32,000. Pay $46,000 (Including Interest) Over 15 Years. Expected Returns Lower
First, let’s calculate the amount of interest Aaron needs to pay per year:
Fixed rate Interest amount
= Loan amount x Yearly loan interest x Number of years
= $40,000 x 1% x 15= $6,000
Total loan amount = $40,000 + $6,000 = $46,000
Yearly payment = $46,000 / 15 = $3,066.67
Initial cash = $32,000
Interest rate = 3.6%
We end up with the following cashflow table:
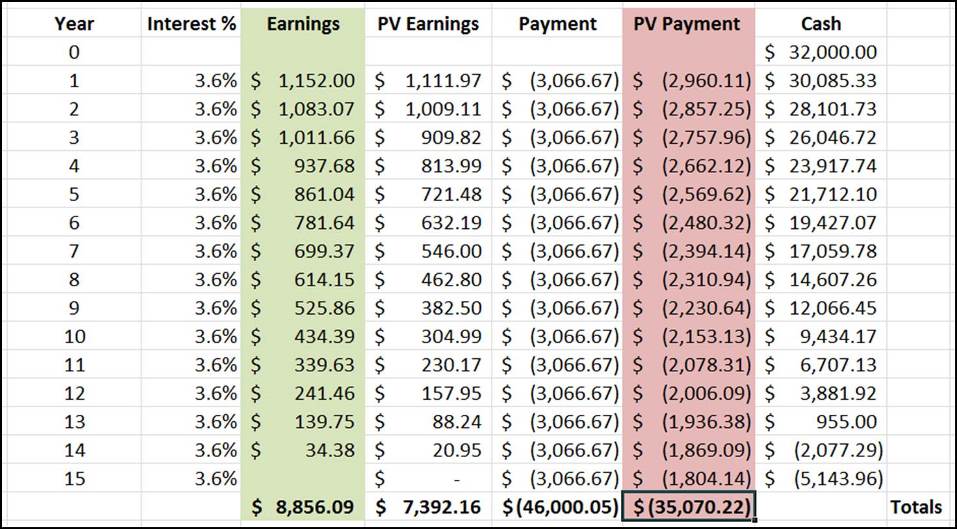
Aaron loses if the expected returns are only 3.6%. It would have been better to take the initial 20% discount:
- Aaron runs out of money in year 14. His investments have not made enough profit to cover the loan payments.
- Total earnings is only $8,856.09. Compare that to the $14,000 we would have saved in Scenario A.
But remember how our first Key Learning was about expected returns? The 3.6% return over 15 years in Scenario B is definitely very conservative. What if Aaron is able to get 5% returns for 15 years?
Scenario C: Invest $32,000. Pay $46,000 (Including Interest) Over 15 Years. Expected Returns Higher
Yearly payment = $46,000 / 15 = $3,066.67
Initial cash = $32,000
Interest rate = 5%
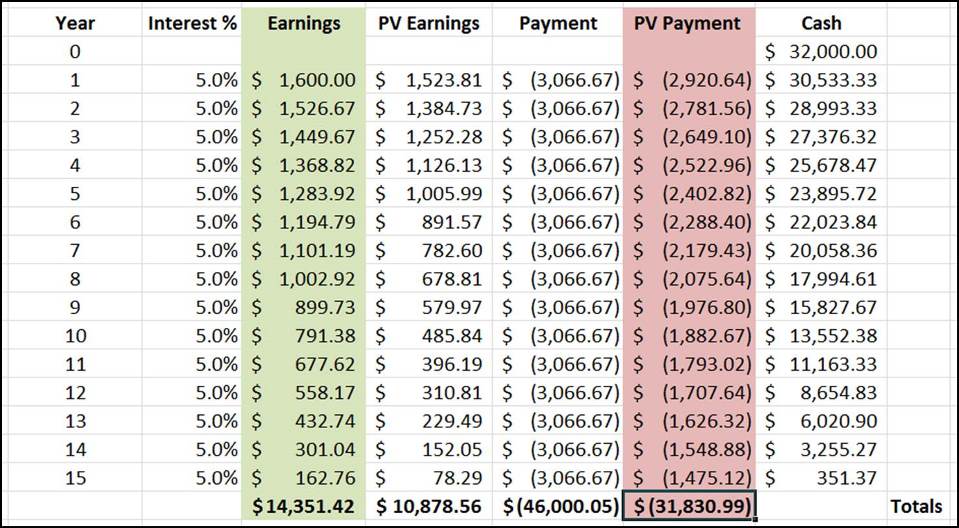
- Aaron has had to pay $14,000 more than in scenario A. Total payment here is $46,000.
- But total earnings from investments is $14,351.42.
- So at the end, Aaron still has $351 left over in the bank.
Scenario C beats Scenario A, even though Aaron has had to pay $14,000 more!
Which doesn’t seem to make sense at first. How do you gain more money over 15 years, despite having to pay $14,000 more?
Here’s another way to look at it: In Scenario C, Aaron invested his $32,000 wisely. Over 15 years, that investment brought in enough money to cover all his debts and make him a small profit. Whereas in scenario A, Aaron said goodbye to his $32,000 in Day One — meaning that he never had the opportunity to make any more money with it.
Key Learning: Compound Interest is Amazing. It can Create Vast Sums of Money over Time
Hypothetical Situation 3:
Aaron owes $60,000 to the Government. They’ll give him a 20% discount if he pays up this week. If not, he has 20 years to pay at 1% interest.
In our final hypothetical situation, we’ll look at what happens if both the time frame and amount are increased. Now that you’re probably tired of my obsession with cashflow tables, we’ll also discuss a quick and easy way to answer the first question I asked today.
But first, let’s again take a look at 3 possible scenarios:
Scenario A: Take the 20% Discount. Pay $48,000 Today
20% discount on $60,000 = $12,000. So we have to pay $48,000 today.
Present Value Payment = $48,000
Savings = $12,000 (immediate) + $12,000 (on interest) = $24,000
Scenario B: Invest $48,000. Pay $72,000 (Including Interest) Over 20 Years. Expected Returns Lower
The amount of interest Aaron needs to pay per year:
Fixed rate Interest amount
= Loan amount x Yearly loan interest x Number of years
= $60,000 x 1% x 20= $12,000
Total loan amount = $60,000 + $12,000 = $72,000
Yearly payment = $72,000 / 20 = $3,600
Initial cash = $48,000
Interest rate = 3.6%
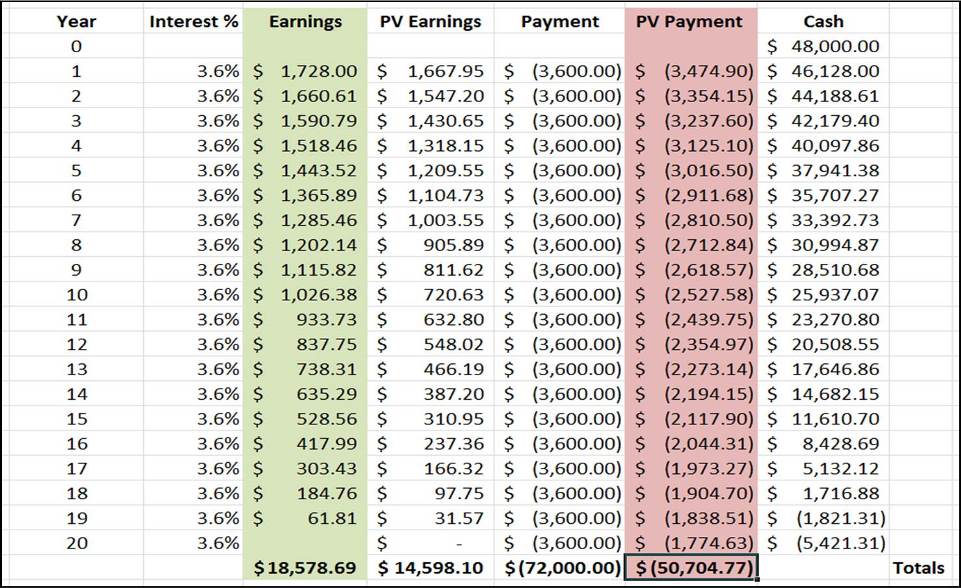
Again, we see that Aaron loses if expected returns are only 3.6%. It would have been better to take the initial 20% discount:
- Aaron runs out of money in year 19. His investments have not made enough profit to cover the loan payments.
- Total earnings is only $18,578.69. Compare that to the $24,000 we would have saved in Scenario A.
Now let’s see what happens if he can make 5% on his investments.
Scenario C: Invest $48,000. Pay $72,000 (Including Interest) Over 20 Years. Expected Returns Higher
Yearly payment = $72,000 / 20 = $3,600
Initial cash = $48,000
Interest rate = 5%
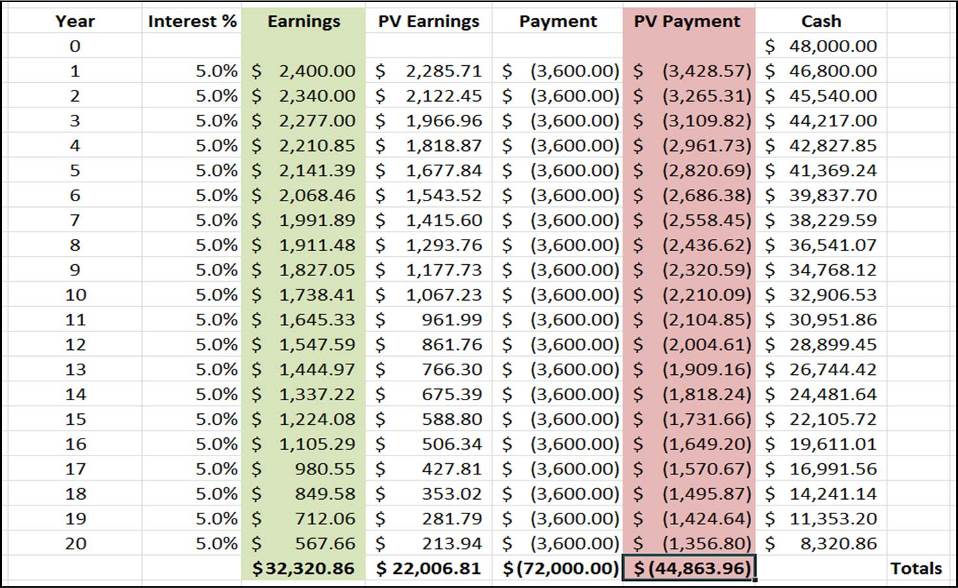
- Aaron has had to pay $24,000 more than in scenario A. Total payment here is $72,000.
- But total earnings from investments is $32,320.86. (recall our second Key Learning — given enough time, compound interest can generate a lot of money)
- So at the end, not only has Aaron paid off his loan, he’s made a nice profit of more than $8K!
(If you like cashflow tables, click here to download the Excel spreadsheet I used to calculate all the examples above. You can use it to simulate your own scenarios, and to check my calculations. Hey, I’m human — let me know if I made a mistake somewhere)
But what if you don’t? What if all these numbers make you dizzy, and all you really want is a simple way to know: Take the discount or not?
The answer lies within the concept of Present Value.
Key Learning: Present Value — the value of a sum of money in the future stated in terms of today’s MONEY.
We’ve just seen how money today can be used to invest, and generate returns in upcoming years. But what if you know you have to pay Y amount of money 5 years from now? What if you had to pay Z amount of money every year for 5 years? How do you compare that to paying X amount of money today?
Use Present Value.
It allows us to evaluate money in the future, based on today’s money.
To evaluate loans, the smart finance people of this world have already come up with a way called Present Value of Annuity.
So, the answer to today’s first question: Take the discount or not?
Compare the Present Value of the Annuity (Loan) to the Present Value of the Lump Sum Payment you have to make today. Choose the option with the lower Present Value.
For example, let’s go back to Hypothetical Situation 3:
Yearly payment = $72,000 / 20 = $3,600
Initial cash = $48,000
Interest rate = 5%
And using the easy financial calculator found on Investopedia to help us:
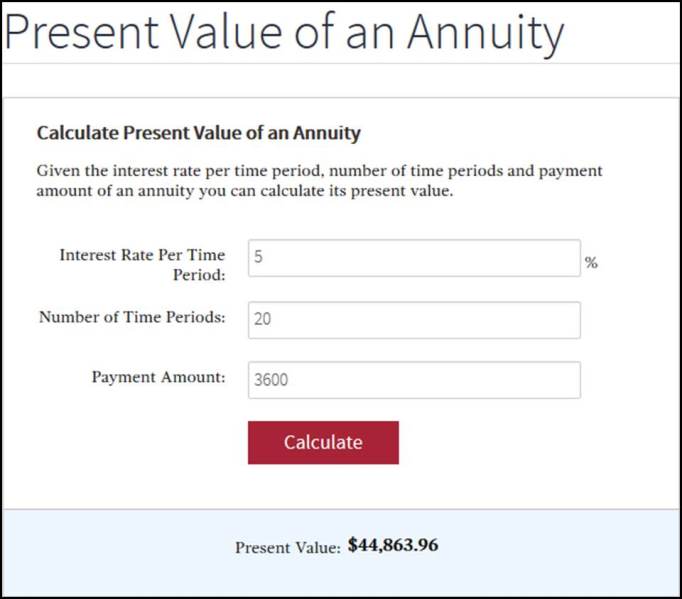
The Present Value of the Loan (if I pay over 20 years) = $44,863.96 (Meaning I’m paying $44,863.96 of today’s dollars).
The Present Value of Payment (if I take the Government’s 20% discount) = $48,000.
So I should choose the loan. Because I would be paying less.
And that, ladies and gentlemen — is how you determine whether you should take a discount or not.
A different version of this article first appeared at iMoney
Further reading: ReadyforZero, Math is Fun, Accounting Coach, Frick CPA
Pic by Rexem at Deviantart




Hello for the PV , should I consider inflation as well? Inflation will affect the future value of the cash and also the PV right?
For these present value calculations, we’re checking what is the value of money in the future based on today’s money. We’ve already included a projected interest rate of either 3.6% or 5%.
Since these “investment” interest rates are typically higher than inflation, you wouldn’t need to additionally factor in inflation.
I cant find the calculator in Investopedia link in the article.
Hi KJ,
Ah I guess the link is broken now, but there are many such calculators online, if you just search for “present value calculator”
Hi,
I am curious to know. Besides inflation, what other factors should I take into account when deciding whether to invest in Fixed Deposit? Should NPV be taken into account?
Hey Ashwynjit,
NPV is used to determine the “today” value of future cashflows. For evaluating fixed deposits, I think a simple comparison between Fixed Deposit interest rate vs inflation rate is sufficient.
Hi! I have about RM48.5K debt with PTPTN and this year is my 6th year and I probably have another 13-14 years to pay off. If PTPTN offer a 20% discount anytime, is it more cost effective for me to take the discount up and pay 1 lump sum? Appreciate if you can advise me as I’m bad with interest calculation!
Hello Veronica,
It depends on the interest rate you are paying to PTPTN. The below link will help you make your decision, once you key in the data:
http://www.investopedia.com/calculator/annuitypv.aspx
All the best!
Hi Aaron,
Could you send me the spreadsheet that you use to simulate some examples on this calculation for housing loan vs FD include the other factor involves to be taken into consideration.
Thanks,
Hi Wong,
About 80% into the article, there’s a link to download the spreadsheet I created. Just search for the words “If you like cashflow tables,”
Hi, I thought paying in discount rate is better for me until I found this article. Because I questions myself if I did the best decision. My debt with PTPTN was around 5000plus and I got discount for 30 %. Even I loss the money, but I have freedom from debt, which is the best decision I made, hopefully
Hi Sanah,
Freedom from debt is a very great feeling isn’t it? Glad that it worked out for you. If I was in the same situation, 5K+ loan, and could get 30% discount — I would probably take it too.
I just wrote this article in case people wanted a “financial calculator” way to calculate “take discount or not?”
That’s a greatly thorough explanation on paying off debt. I think it boils down two things:
1. Your monthly / annual cash flow
2. Your fiscal discipline
I wouldn’t mind paying off the loan first at a discounted rate but I need to make sure any amount of money that I earned in the following months is wisely invested rather than spent.
Thanks for dropping by Danial,
You certainly said that right: cash flow and discipline. The two most important things for personal finance…
Hi Aaron,
Been a silent reader and love your resourceful blog!
I have been wondering this and thanks for all the calculation and scenarios! Have you ever thought apply the case on housing loan? As you may aware, we have the semi-flexi housing loan, which allows to deposit any extra money to reduce the interest on the total loan account. However, I always have doubt, say if I have 200K now and the house is 300K for 30 years:
1) Should I deposit in 200K in the loan account? so I could pay less interest and more on principal
2) Or put 200k in FD, because FD has a higher rate than loan interest?
Thank you!
1)
Hi Richard,
Thanks for your kind words and the great question.
Yes, I’ve some of my own calculations on calculating housing loan vs FD. In my experience, housing loan interest is always higher than FD rate. (Intuitively this makes sense, because banks will always charge you more to lend you money, compared to giving you interest for keeping your money). So, the quick answer is putting it into Loan Amount is better than FD, in terms of returns.
There are other factors involved of course. When you say semi-flexi, I believe that withdrawing the money out from the loan isn’t very straightforward — so you need to consider whether you need that money quickly or not.
Let me look through my files and also email you a spreadsheet I use to simulate some examples on this calculation…